
Ir a página:

LA RESPUESTA:

6. Anoten sobre la línea si el enunciado es falso o verdadero. Si consideran que es falso, den un ejemplo.
a) Si un número positivo se eleva al cuadrado y al resultado se le extrae raíz cuadrada, se llega al número original. _________
b) Si un número negativo se eleva al cuadrado y al resultado se le extrae raíz cuadrada, se llega al número original. _________

a) Sí, por ejemplo, 52=25, la raíz de 25 es 5.
b) No, por ejemplo, -52=25, la raíz de 25 es 5, no -5.
1. Trabajen en pareja. Anteriormente estudiaron un procedimiento para encontrar la raíz cuadrada de un número mediante aproximaciones sucesivas. A continuación analizarán otro procedimiento para encontrar las cifras de la parte entera cuando se requiere calcular la raíz cuadrada de un número que no es cuadrado perfecto. Por ejemplo, encontrar la parte entera de la raíz cuadrada de √4528
a) Hay que determinar cuántas cifras tendrá la parte entera de la raíz. Comenten entre ustedes y con otros equipos por qué no es posible que tenga tres cifras.

La raíz cuadrada de 4528 tendrá dos cifras en su parte entera.
Un número con tres cifras al cuadrado resultaría en un valor mucho mayor que 4528, ya que 100 al cuadrado es 10000, lo cual tiene cinco cifras.




b) La parte entera de la raíz tiene dos cifras, por lo tanto, es de la forma 10a+b. El término 10a representa las decenas y b representa las unidades. Eleven ese número al cuadrado: (10a+b)2 = (10a+b)(10a+b) =_____

Al elevar al cuadrado un número de la forma 10a+b, donde a y b son las cifras de las decenas y las unidades respectivamente, obtenemos:
(10a+b)2 = 100a2 + 20ab + b2




1. Aplicar la fórmula del binomio al cuadrado: La fórmula es (x+y)2=x2+2xy+y2, donde x y y serían 10a y b, respectivamente.
2. Efectuar la operación de elevar al cuadrado cada término y multiplicar cruzado:
3. Sumar los resultados: Esto significa sumar los tres términos obtenidos en el paso anterior.
c) Para encontrar la cifra de las decenas, usamos el término 100a2 del resultado anterior. Encuentren esa cifra completando la primera tabla de la siguiente página.
¿Para qué valor de a el valor numérico de 100a2 es mayor que 4528?
Esto significa que la mejor aproximación por defecto (esto es, por abajo de 4528) se produce cuando a=6. Esta es la cifra de las decenas de la parte entera que se busca.

La tabla se completa de la siguiente manera: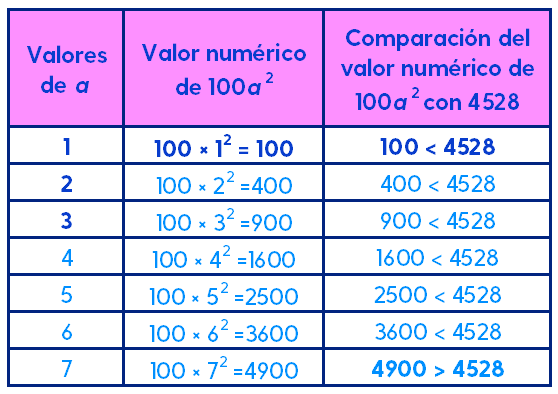
¿Para qué valor de a el valor numérico de 100a2 es mayor que 4528?
El valor numérico de 100a2 es mayor que 4528 para el valor de a=7

Para llenar la tabla calculamos 100a2 para los valores de a del 1 al 7, elevando cada número al cuadrado y multiplicando por 100 el resultado.
Luego comparamos cada resultado de 100a2 con 4528 para determinar si es menor.
Identificamos el valor máximo de a para el cual 100a2 aún es menor que 4528.