Matemáticas
Razones Trigonométricas
RAZONES TRIGONOMÉTRICAS MATEMÁTICAS 3° SECUNDARIA
Para el estudio de este tema, es necesario revisar algunos conceptos básicos que tienen que ver con su contenido.
La trigonometría es la rama de las matemáticas que estudia los triángulos y sus relaciones, especialmente el triángulo rectángulo.
Una razón o función trigonométrica resulta de la relación entre los lados de un triángulo rectángulo con respecto a uno de los ángulos agudos.
Un triángulo rectángulo es aquel que tiene un ángulo recto (90°) y dos ángulos agudos.

Los lados que forman el ángulo recto del triángulo rectángulo se llaman catetos y de acuerdo al ángulo que se tome de referencia, reciben el nombre de cateto opuesto o cateto adyacente.
En la figura del ejemplo 1, se está tomando como referencia el ángulo “A” que mide 25°, por ese motivo, el lado que le queda enfrente se llama cateto opuesto y el lado que le queda contiguo, se llama cateto adyacente.
El lado más grande del triángulo rectángulo y que se ubica enfrente del ángulo recto, se llama hipotenusa.
En la imagen del ejemplo 2, el ángulo que se toma como referencia es “A” que mide 45° y se observan claramente los catetos opuesto y adyacente.
Las tres razones básicas de la trigonometría son el seno, el coseno y la tangente.
Más allá de la tangente, el seno y el coseno, es posible reconocer otras razones trigonométricas que se utilizan menos, como la cotangente, la cosecante y la secante.
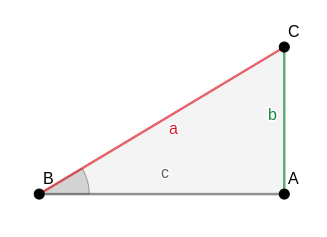
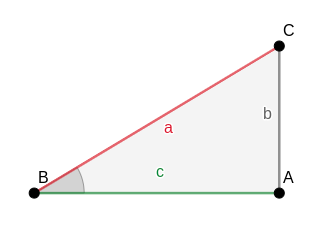
Razones trigonométricas en un triángulo rectángulo

Seno
El seno del ángulo “B” es la razón entre el cateto opuesto al ángulo y la hipotenusa. Se denota por sen B.


Coseno
El coseno del ángulo “B” es la razón entre el cateto adyacente al ángulo y la hipotenusa. Se denota por cos B.


Tangente
La tangente del ángulo “B” es la razón entre el cateto opuesto al ángulo y el cateto adyacente al ángulo. Se denota por tan B.
Cosecante
La cosecante del ángulo “B” es la razón inversa del seno de B. Se denota por csc B.
Secante
La secante del ángulo B es la razón inversa del coseno de B. Se denota por sec B.

Cotangente
La cotangente del ángulo B es la razón inversa de la tangente de B. Se denota por cot B.
En resumen, las 6 funciones trigonométricas quedan de la siguiente manera.

Ejemplo 1:
En un triángulo rectángulo, los lados mayores miden 13 cm. y 12 cm. Calcula las razones trigonométricas del menor ángulo.

En un triángulo rectángulo el lado más pequeño se opone al ángulo más pequeño, por lo tanto, el menor ángulo es “A” que se opone al lado más pequeño BC
Los lados mayores son: AC = 13 cm. y AB = 12 cm.
Aplicando el teorema de Pitágoras se puede encontrar la medida del lado BC
El teorema de Pitágoras se representa: (AC)2 = (BC)2 + (AB)2
Donde AC es la hipotenusa y los catetos son BC y AB
Haciendo la sustitución en la fórmula por los valores conocidos, nos queda:
(BC)2 + (12)2 = (13)2
(BC)2 + 144 = 169
(BC)2 = 169 – 144
(BC)2 = 25

BC = 5
Ahora podemos definir las funciones trigonométricas:
sen A = 5/13 cos A = 12/13 tan A = 5/12
csc A = 13/5 sec A = 13/12 cot A = 12/5
Ejemplo 2:
Dada la medida del ángulo se encuentra el valor de la función trigonométrica.
sen 25°= co/h = 2.8/6.62 = 0.422
cos 25°= ca/h = 6/6.62 = 0.906
tan 25° = co/ca = sen/cos = 2.8/6 = 0.466
En conclusión, las razones trigonométricas son una herramienta de las matemáticas, que al igual que el teorema de Pitágoras, tiene como propósito principal el cálculo de los valores o distancias de los catetos o de la hipotenusa, pero involucrando el valor de sus ángulos internos, y por ello también es posible calcularlos a través de los otros valores.


